uhull

A simple (but not simpler) algorithm for concave hull of 2D point sets using an alpha shape algorithm.

Note

• uhull! (Brazil) yeah! (expresses joy or celebration)

Installation

pip install uhull

Concave hull for geographic coordinate points

• Interactive map of points in Rio de Janeiro, Brazil

• Interactive map of points in Brasília, Brazil

• Interactive map of points in Pará, Brazil

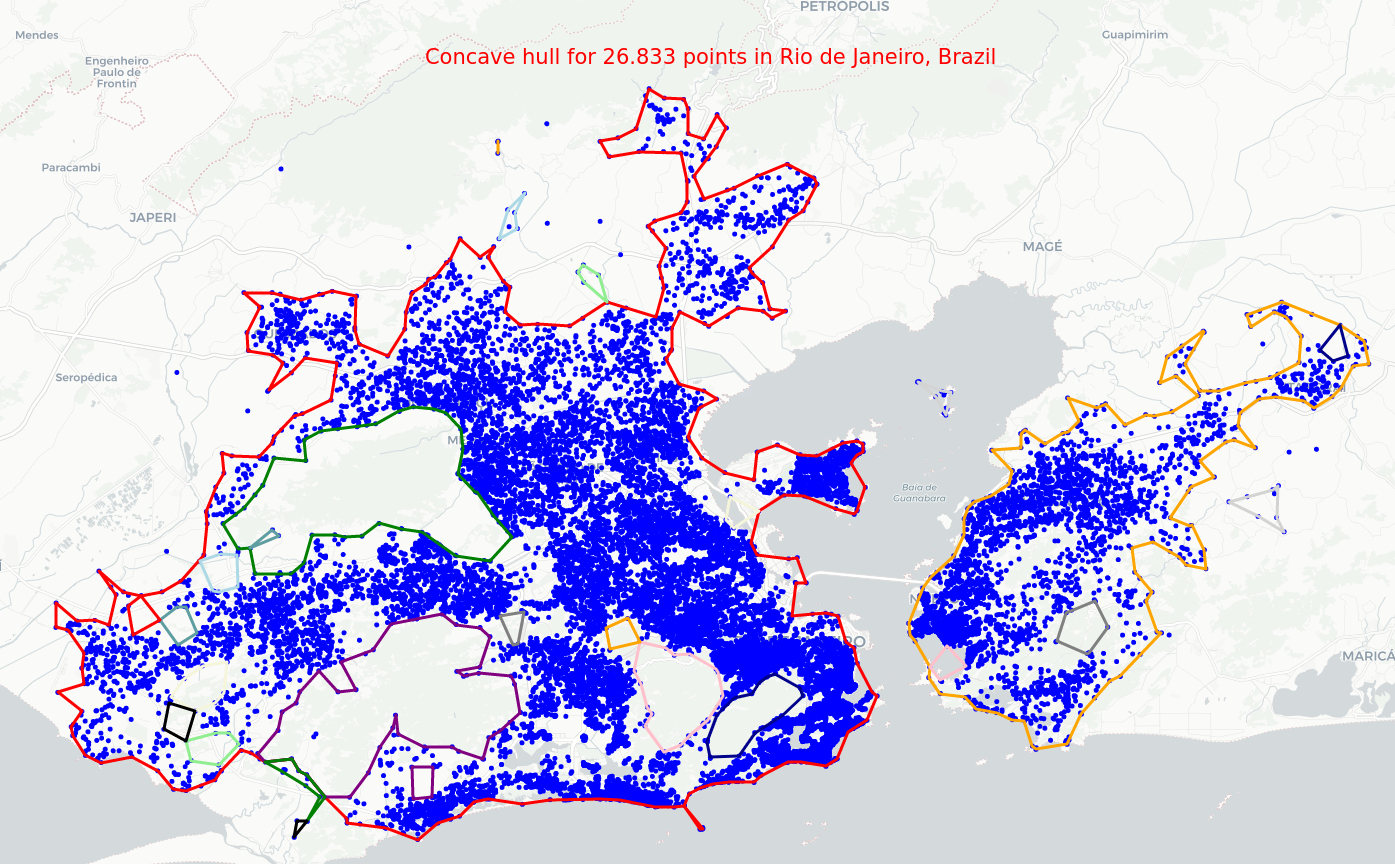
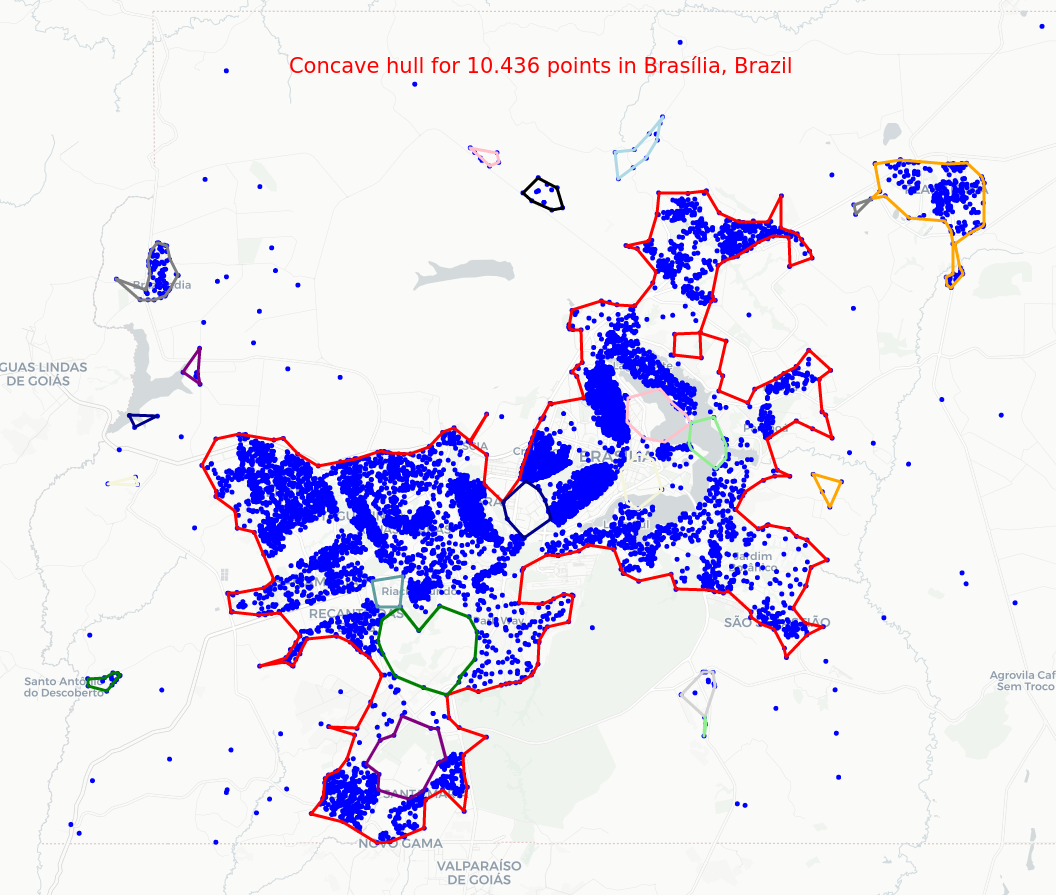
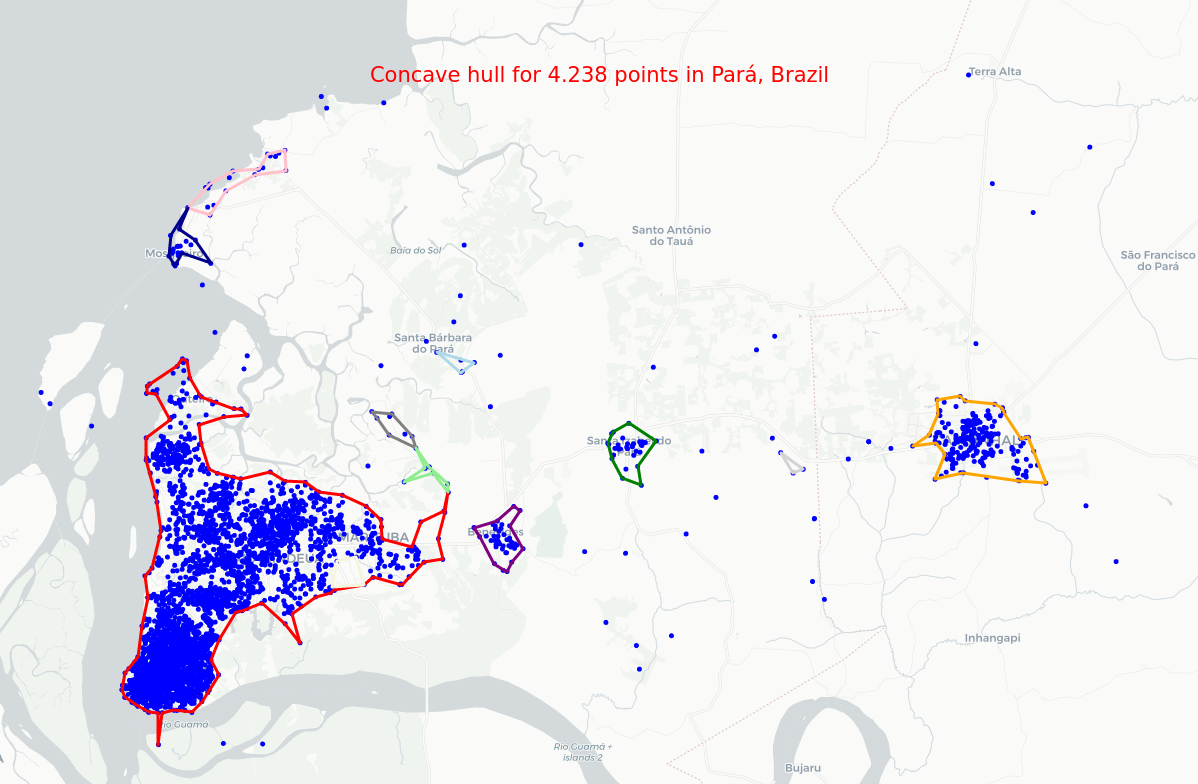
• You can find the code to generate the interactive maps here.

Quickstart

Concave hull for 2D points

Suppose we want to find a concave hull for the following set of points:

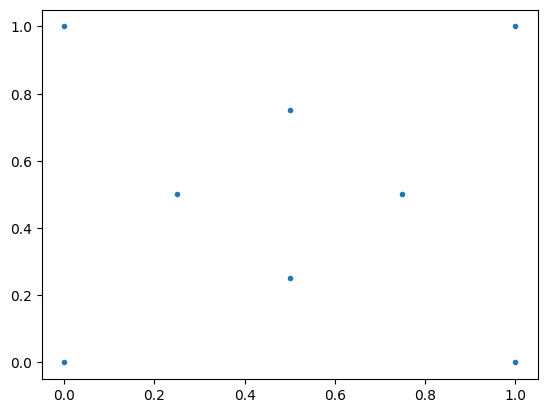
We can find the polygons that form the concave hull of the set as follows:

from uhull.alpha_shape import get_alpha_shape_polygons

points = [
    (0.0, 0.0),
    (0.0, 1.0),
    (1.0, 1.0),
    (1.0, 0.0),
    (0.5, 0.25),
    (0.5, 0.75),
    (0.25, 0.5),
    (0.75, 0.5),
]
polygons = get_alpha_shape_polygons(coordinates_points=points)

The concave hull obtained for these points is formed by a single polygon as follows:

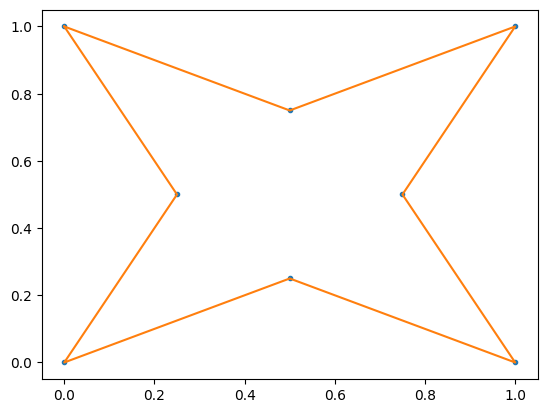
Note

Two parameters influence the concavity of the concave hull polygons: a non-negative numerical value alpha and the function to measure the distance between the 2D points. By default alpha is set to 1.5 and the function to measure distance is Haversine. The length of the edges of the polygons generated by the algorithm is calculated using the informed distance function. The alpha parameter defines the size of the range of acceptable values for the length of these edges that we must consider in the algorithm. Thus, larger alpha considers larger edges in the algorithm, resulting in a smaller number of polygons to represent the concave hull and consequently we obtain a less concave (or, more convex) hull.

As an example, notice that by doubling the default value of alpha, we get the convex hull:

from uhull.alpha_shape import get_alpha_shape_polygons

points = [
    (0.0, 0.0),
    (0.0, 1.0),
    (1.0, 1.0),
    (1.0, 0.0),
    (0.5, 0.25),
    (0.5, 0.75),
    (0.25, 0.5),
    (0.75, 0.5),
]
polygons = get_alpha_shape_polygons(coordinates_points=points, alpha=2 * 1.5)

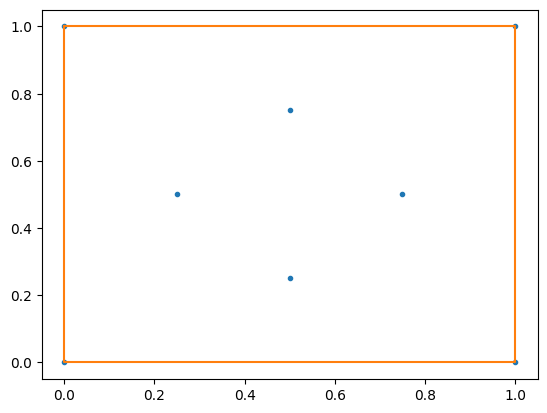
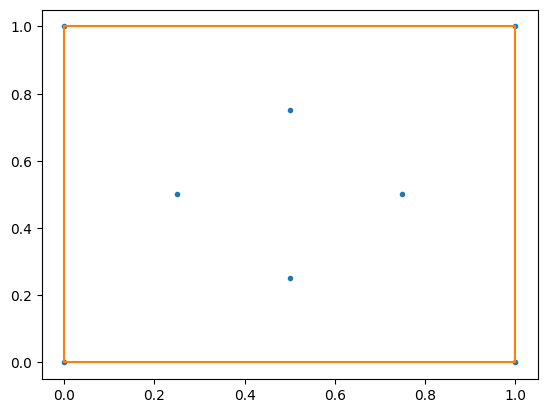
As another example let's define a distance function and get concave hull with it.

from uhull.alpha_shape import get_alpha_shape_polygons


def manhattan_distance(coord1, coord2):
    return abs(coord1[0] - coord2[0]) + abs(coord1[1] - coord2[1])


points = [
    (0.0, 0.0),
    (0.0, 1.0),
    (1.0, 1.0),
    (1.0, 0.0),
    (0.5, 0.25),
    (0.5, 0.75),
    (0.25, 0.5),
    (0.75, 0.5),
]
polygons = get_alpha_shape_polygons(
    coordinates_points=points, distance=manhattan_distance
)

• You can find code to generate quickstart images here.

GitHub

• Repository